TLA+でハードに死なないために パート1

目次

• はじめに
• $TLA^+$の紹介
• $TLA^+$における状態機械
• リソースとツール
• モデルチェック
  • 振る舞い仕様
  • モデル
• ダイ・ハード
• 参考文献

はじめに

これは、レスリー・ランポートによる「TLA+入門」コースのコンスペクトの一連のブログ投稿の最初のものです。コースの構成に直接従い、コース教材に追加の情報や説明を加えることで、コースを受講している方々にとって良い参考になるでしょう。したがって、すべての功績はレスリー・ランポートと彼のウェブサイトで見つけることができる彼のコースにあります。

$TLA^+$は時相論理に基づいていますので、スマートコントラクトのセキュリティにおけるLTLとCTLの応用のブログ投稿を読むことができます。

$TLA^+$の紹介

$TLA^+$は、高レベル（コードの上位、設計レベル）のシステム（モジュール、アルゴリズムなど）のモデリング言語であり、以下のコンポーネントで構成されています。

• TLC — モデルチェッカー
• TLAPS — $TLA^+$の証明システム
• $TLA^+$ Toolbox — IDE

$TLA^+$システムは、デジタルシステムの重要な部分をモデル化するために使用され、重要度の低い部分や低レベルの実装の詳細を抽象化します。$TLA^+$は、並行および分散システムを設計するために設計され、テストでは見つけにくい設計エラーを発見し修正するのに役立ちます。そして、コードを一行も書く前にそれを行います。

OpenComRTOSは、商用のネットワーク中心のリアルタイムオペレーティングシステムであり[3]、設計と開発プロセスの中で$TLA^+$を大いに活用し、その経験を無料で入手可能な書籍で共有しました[4]。そして、設計を使用することでコードベースのサイズとエラーの数を大幅に削減し、エンジニアリングの視点を全体的に向上させることを示しました。

結果として、$TLA^+$はプログラマーやエンジニアに新しい思考方法を提供し、$TLA^+$が役に立たない場合でもより優れたプログラマーやエンジニアにします。$TLA^+$はエンジニアにより抽象的に考えることを強制します。

抽象化 — 関連性のない詳細を取り除くプロセスであり、エンジニアリングの最も重要な部分です。これなしでは、小さなシステムを設計し理解することはできません。

多くの人が日常的に使用しているシステムを検証するために$TLA^+$を使用している大企業の例として、Amazon Web Servicesがあります。彼らは$TLA^+$を使用して、分散アルゴリズムとAWSシステム設計の正確性を検証しています[5]。分散システムにおけるアルゴリズムと通信の問題は、レスリー・ランポートの論文「分散システムにおける時間、クロック、およびイベントの順序付け」でよく説明されています[6]。

システム設計は、_仕様_と呼ばれる正式な方法で表現されます。

仕様 — 正確な高レベルのモデル。

$TLA^+$は仕様を定義しますが、コードを生成することはできません。しかし、より明確なアーキテクチャを考案し、より正確で精密な、場合によってはコンパクトなコードを書くのに役立ちます。個々の実行に対する条件を表現する特性をチェックすることができます（システムが特性を満たすのは、すべての実行がそれを満たす場合に限ります）。

$TLA^+$の基礎となる抽象化は以下の通りです。システムの実行は一連の離散的なステップとして表され、ステップはある状態から次の状態への変化です。

• 離散的 — 連続的な進化は一連の離散的なイベントです（コンピュータは離散的なイベントベースのシステムです）。
• シーケンス — 並行システムはシーケンシャルなプログラムでシミュレートできます。
• ステップ — 状態の変化。
• 状態 — 変数への値の割り当て。

振る舞い — 状態のシーケンス。

$TLA^+$システムのコンテキストでの状態機械は、以下によって記述されます。

1. すべての可能な初期状態 — [変数が何であるか] と [それらの可能な初期値]。
2. 任意の与えられた状態に続く可能な次の状態 — 現在の状態での値と次の状態での可能な値との関係。
3. 次の状態が可能でない場合、停止します。

制御状態 — 次に実行されるステートメント。

状態機械は低レベルの実装の詳細を排除し、$TLA^+$は状態機械を記述するための言語です。

$TLA^+$における状態機械

$TLA^+$は普通のシンプルな数学を使用します。次のCコードのために定義された状態機械の例を考えてみましょう。

int i;
void main()
{
    i = someNumber();
    i = i + 1;
}

このコードを$TLA^+$の状態機械の定義に変換するためには、このコードの実行フローを状態（変数の集合）にパックする必要があります。この例では、i変数を定義する方法は明らかです。しかし、制御状態もインスタンス化する必要があります。それをpcと呼び、以下のようにします。

• pc = "start" は i = someNumber(); に対応
• pc = "middle" は i = i + 1; に対応
• pc = "done" は実行が終了したことを示す

この例では、someNumber()は[0:1000]の範囲から整数を返すと仮定します。

システムを定義するためには、システムの_初期_状態と、現在の状態から到達可能な_次の_システム状態を定義する必要があります。

これは上記のCコードの式であり、実行のシーケンスではありません。

• 初期状態の式：(i = 0) /\ (pc = "start")
• 次の状態の式：

\/    /\ pc = "start"
      /\ i' \in 0..1000
      /\ pc' = "middle"
\/    /\ pc = "middle"
      /\ i' = i + 1
      /\ pc' = "done"

これは式であるため、交換法則や結合法則などの式の性質を尊重します。

サブ式は、仕様をよりコンパクトにするために、それぞれ独自の定義に抽出することもできます。

A == /\ pc = "start"
     /\ i' \in 0..1000
     /\ pc' = "middle"

B == /\ pc = "middle"
     /\ i' = i + 1
     /\ pc' = "done"

Next == A \/ B

この仕様から、_初期_状態から到達可能な2つの可能な_次の状態_があることがわかります。Aは実行の開始を示し、iに数値を割り当て、次のpc状態（p'と等しい）に移動します。Bはiをインクリメントし、最終状態に移動します。

リソースとツール

$TLA^+$の学習リソースは多くありませんが、いくつか言及すべきものがあります。

• Learning TLA+ — 有用なリンクを含むポータル
• TLA+ toolbox binaries — Javaベースの$TLA^+$ IDE
• pdflatex — pdfをレンダリングするために必要なコンポーネント

モデルチェック

さて、TLCとモデルチェックに関連するトピックについて話しましょう。

TLCは仕様によって許可されるすべての可能な振る舞いを計算します。より正確には、TLCは仕様のモデルをチェックします。

• TLCは、実行が予期せず停止した場合、デッドロックを報告します。
• TLCは、実行が予期通りに停止した場合、終了を報告します。

$TLA^+$は定理とその定理の正式な証明を書くことを可能にします。TLAPS（TLA証明システム）はそれらの証明をチェックするためのツールであり、アルゴリズムの正確性の証明をチェックすることができます。

実際には、spec（仕様）という用語は以下を意味します。

1. モジュールのセット。インポートされたモジュールを含む.tlaファイルで構成されます。
2. 指定されたシステムまたはアルゴリズムの可能な振る舞いを記述する$TLA$式。

仕様には複数のモデルを含めることができます。モデルはTLCに何をすべきかを伝えます。モデルで明示的に選択する必要がある部分は以下の通りです。

• 振る舞い仕様とは何か（振る舞い仕様は、チェックしたいシステムまたはアルゴリズムの可能な振る舞いを記述する式または式のペアです）。
• TLCがチェックすべきこと。
• 定数パラメータに代入する値。

振る舞い仕様

振る舞い仕様を書く方法は2つあります。

1. InitとNext
   • 初期状態と次の状態の関係をそれぞれ指定する式のペア。
2. 単一の式
   • $Init \land [][Next]_{vars} \land F$の形式の単一の時相式。ただし、
     • $Init$は初期述語。
     • $Next$は次の状態の関係。
     • $vars$は変数のタプル。
     • $F$はオプションの公正性の式。

公正性を含む振る舞い仕様を書く唯一の方法は時相式を使用することです。そうでない場合、仕様には変数がなく、この場合、TLCは仮定をチェックし、定数式を評価します。

TLCがチェックできる振る舞い仕様の特性は3種類あります。

• デッドロック — 次の状態の関係が後続の状態を許可しない状態でデッドロックが発生したと言います。
• 不変条件 — 到達可能なすべての状態で真である状態述語。つまり、振る舞い仕様で許可される振る舞いで発生する可能性のある状態。
• 特性 — TLCは、振る舞い仕様が時相論理式として表現される時相特性を満たす（暗黙的に含む）かどうかをチェックできます。

モデル

モデルの最も基本的な部分は、宣言された定数への値の割り当てのセットです。

通常の割り当て

定数の値を、仕様で定義された記号のみを含む任意の定数$TLA^+$式に設定できます。その式には宣言された定数を含めることもできますが、その定数に割り当てられる値がその定数に依存しない限りです（循環依存を避けます）。モデルはすべての宣言された定数の値を指定する必要があります。

モデル値

モデル値は、TLCが$TLA^+$で表現できる任意の値と等しくないと見なす未指定の値です。例えば、Procに3つのモデル値の集合{p1, p2, p3}を代入することができます。誤ってp+1のような式を書いた場合、pの値がプロセスである場合、TLCはその式を評価しようとしたときにエラーを報告します。なぜなら、プロセスはモデル値であり、数値ではないことを知っているからです。Procにモデル値の集合を代入する重要な理由は、TLCが対称性を活用できるようにすることです。

例: NotANat == CHOOSE n : n \notin Nat

これはNotANatを自然数でない任意の値に定義します。TLCは無限のCHOOSE式を評価できないため、この定義を評価できません。TLCが仕様を扱えるようにするためには、NotANatにモデル値を代入する必要があります。代入する最良のモデル値はNotANatという名前のものです。これは定義のオーバーライドによって行われます。$TLA^+$ Toolboxは、上記の正確な構文または以下の構文を持つ定義を見つけた場合、モデルを作成するときにそのセクションに適切なエントリを作成します。 NotANat == CHOOSE n: ~(n \in Nat)。ここで、Natは任意の式であり、NotANatとnは任意の識別子であり得ます。

モデル値は次のように型付けできます。モデル値は名前が2文字のT_で始まる場合に限り、型Tを持ちます。

モデルで宣言されたモデル値は、モデルの仕様の任意の式で通常の値として使用できます。

対称性

メモリシステムの仕様を考え、そのシステムは宣言された定数Valを含み、メモリレジスタの可能な値の集合を表します。値の集合Valは、おそらくメモリシステムの振る舞い仕様に対する対称性集合であり、値の集合の要素を置換しても、その振る舞いがその振る舞い仕様を満たすかどうかは変わりません。TLCはこれを利用してチェックを高速化できます。Valにモデル値の集合{v1, v2, v3}を代入するとします。対称性集合オプションを使用して、このモデル値の集合を振る舞い仕様の対称性集合であると宣言できます。これにより、TLCが調べる必要のある到達可能な状態の数を最大で3!、すなわち6まで減らすことができます。

複数のモデル値の集合を対称性集合として宣言できます。ただし、すべての対称性集合の合併には、異なる型の2つの型付きモデル値を含めることはできません。

TLCは、あなたが対称性集合として宣言した集合が本当にそうであるかどうかをチェックしません。もし対称性集合でない集合を対称性集合として宣言した場合、TLCはそれ以外の場合に見つけるエラーを見つけられない可能性があります。式は、集合Sに対して、Sの任意の2つの値を入れ替えても式の値が変わらない場合に限り、Sに対して対称的です。例えば、式{{v1, v2}, {v1, v3}, {v2, v3}}は集合{v1, v2, v3}に対して対称的です。例えば、この式でv1とv3を入れ替えると{{v3, v2}, {v3, v1}, {v2, v1}}となり、これは元の式と等しいです。モデルが指定する定数や定義された演算子への代入が行われた後、仕様とチェックしているすべての特性がSに対して対称的である場合にのみ、モデル値の集合Sを対称性集合として宣言すべきです。例えば、モデルがある定数にv1を代入する場合、{v1, v2, v3}を対称性集合として宣言すべきではありません。$TLA^+$の演算子のうち、対称的な式に適用したときに非対称的な式を生成する可能性があるのはCHOOSEだけです。例えば、式CHOOSE x \in {v1, v2, v3} : TRUEは{v1, v2, v3}に対して対称的ではありません。

対称性集合はライブネス特性をチェックするときに使用すべきではありません。これにより、TLCはエラーを見つけられなくなったり、存在しないエラーを報告する可能性があります。

ダイ・ハード

「ダイ・ハード」は1988年のアクション映画です。この映画では、主人公たちが2つの水差しを使って問題を解き、爆弾を無効化するシーンがあります。問題は、3ガロンと5ガロンの水差しを使って4ガロンの水を測ることです。

プロットについては、「ダイ・ハード 水差し問題」をYouTubeで検索するか、ここをクリックしてください🙂。この問題を$TLA^+$を使って解決します。

まず、振る舞いを書き出す必要があります。$small$と$big$の値がそれぞれの水差しのガロン数を表すとします。

水差しを満たすことは単一のステップであり、中間的なステップはありません。

実際の仕様は、いくつかの種類のエラーを排除するために書かれます。

$TLA^+$には型宣言はありませんが、型の正確性を主張する式を定義することが重要です。これは仕様を理解するのに役立ち、TLCはそのような式が常に$true$であるかどうかをチェックすることで型をチェックできます。

TypeOK == /\ small \in 0..3
          /\ big   \in 0..5

ここでは、smallが[0:3]の範囲の整数であり、bigが[0:5]の範囲の整数であることを定義しています。しかし、この定義は仕様の一部ではありません。

初期状態の式 Init == small = 0 /\ big = 0 はシステムの初期状態を定義します。 次の状態の式 は状態から状態への可能な遷移を定義し、通常は $F_1 \lor F_2 \lor … \lor F_n$ と書かれ、各式 $F_i$ は異なる種類のステップを許可します。

この問題には3種類のステップがあります。

• 水差しを満たす
• 水差しを空にする
• 一方の水差しからもう一方の水差しに水を注ぐ

仕様は次のように定義します。

Next == \/ FillSmall  \* 小さい水差しを満たす
        \/ FillBig    \* 大きい水差しを満たす
        \/ EmptySmall \* 小さい水差しを空にする
        \/ EmptyBig   \* 大きい水差しを空にする
        \/ SmallToBig \* 小さい水差しから大きい水差しに水を注ぐ
        \/ BigToSmall \* 大きい水差しから小さい水差しに水を注ぐ

定義の名前（FillSmallなど）は、使用する前に定義されている必要があります（Nextの定義より前に）。

FillSmall == /\ small' = 3
             /\ big' = big

式を定義するときには、システム全体として考え、ステップをある状態から別の状態への遷移として考えることを念頭に置く必要があります。我々の場合、FillSmallをFillSmall == small' = 3と定義することはできません。なぜなら、この式はプログラム状態の2番目の部分（big）を定義する部分がないからです。言い換えれば、この式はsmall'が3であり、big'が何でもよい場合に$true$になります。しかし、これは正しくありません。実際には、小さい水差しを満たす場合、大きい水差しは変化せずそのままの状態にあります。

次に、SmallToBigを定義します。考慮すべき2つの可能なケースがあります。

SmallToBig == /\ IF big + small <= 5
                  THEN /* 余裕がある -> 小さい水差しを空にする
                  ELSE /* 余裕がない -> 大きい水差しを満たす

SmallToBig == /\ IF big + small <= 5
                  THEN /\ big' = big + small
                       /\ small' = 0
                  ELSE /\ big' = 5
                       /\ small' = small - (5 - big)

------------------------------ MODULE DieHard ------------------------------
EXTENDS Integers

VARIABLES small, big

TypeOK == /\ small \in 0..3
          /\ big \in 0..5

Init == /\ big = 0
        /\ small = 0

FillSmall == /\ small' = 3
             /\ big' = big

FillBig == /\ big' = 5
           /\ small' = small

EmptySmall == /\ small' = 0
              /\ big' = big

EmptyBig == /\ big' = 0
            /\ small' = small

SmallToBig == IF big + small =< 5
                THEN /\ big' = big + small
                     /\ small' = 0
                ELSE /\ big' = 5
                     /\ small' = small - (5 - big)

BigToSmall == IF big + small =< 3
               THEN /\ big' = 0
                    /\ small' = big + small
               ELSE /\ big' = big - (3 - small)
                    /\ small' = 3

Next == \/ FillSmall
        \/ FillBig
        \/ EmptySmall
        \/ EmptyBig
        \/ SmallToBig
        \/ BigToSmall

=============================================================================

この仕様に対してモデルを作成して実行すると、エラーがないことがわかります。これは良いことですが、仕様の特定の不変条件をチェックしているわけではありません。

不変条件とは、到達可能なすべての状態で$true$である式です。

TypeOKをsmallとbigの型定義として定義しましたので、この式を不変条件として追加し、この不変条件が破られないことを確認できます。

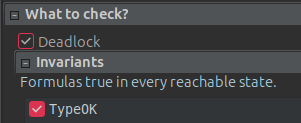
これを実行すると、依然としてエラーは表示されず、smallとbigが到達可能なすべての状態でその型を尊重していることを意味します。

次に、bigに正確に4ガロンの水を注ぐという_ダイ・ハード_の問題を解決できます。そのために、新しい不変条件big /= 4を不変条件セクションに追加します。

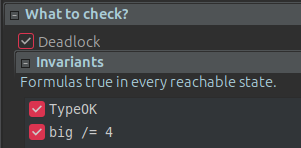
ここで、この不変条件は反例として機能します。不変条件は、すべての到達可能な状態で$true$になる式です。我々はbig = 4となる状態（実際には状態のシーケンス）を見つける必要がありますので、/=記号を使用してこれを否定します。新しい式でモデルを実行すると、エラーが見つかり（不変条件が破られる状態が見つかり）、その状態に至る状態のシーケンスが表示されます。

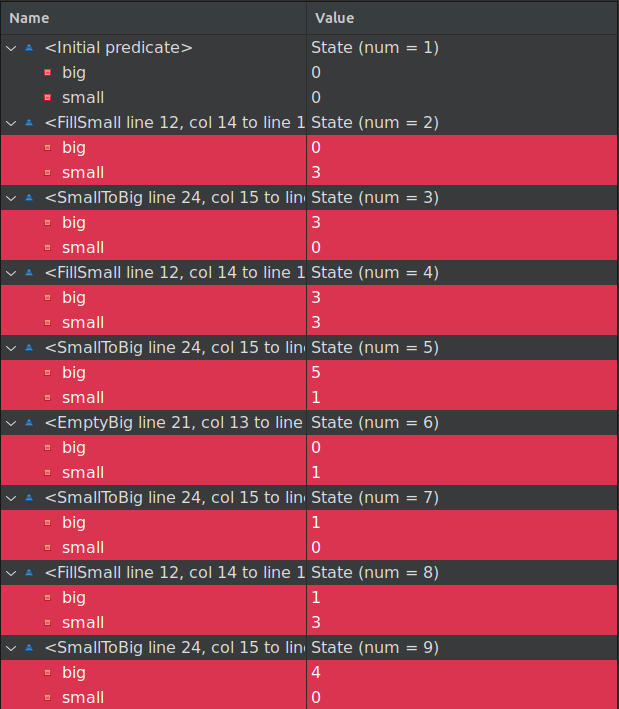
これで、問題を解決するために必要な正確なステップを見ることができ、主人公たちは先に進むことができます。

参考文献

• Leslie Lamport. Learning TLA+
• スマートコントラクトのセキュリティにおけるLTLとCTLの応用
• OpenComRTOS
• Eric Verhulst, Raymond T. Boute, José Miguel Faria, Bernhard H C Sputh, Vitaliy Mezhuyev. Formal Development of a Network-Centric RTOS. January 2011. DOI:10.1007/978-1-4419-9736-4. ISBN: 978-1-4419-9735-7
• Chris Newcombe, Tim Rath, Fan Zhang, Bogdan Munteanu, Marc Brooker and Michael Deardeuff. Amazon Web Servicesが形式手法をどのように使用しているか。2015年、Communications of the ACM
• Leslie Lamport. 分散システムにおける時間、クロック、およびイベントの順序付け。1978年。Massachusetts Computer Associates, Inc.

このブログ記事の議論に参加してください: